Robot dynamic reconfigurability

1. Analysis of the degeneracy conditions of parallel robot dynamic models

In order to increase the workspace size of parallel robots, limited due to the presence of singularities, several approaches have been envisaged in the literature, such as:

• The design of parallel robots without singularities. This can be done by using the optimal design approach or by creating fully-isotropic mechanisms (which have no Type 2 singularities but usually have LPJTS (leg passive joint twist system) singularities). This solution is the most usual one, but it usually leads to the design of robots with a small workspace size or robot architectures with very low practicability.
• The use of redundancyor, to reduce costs, the use of mechanisms with variable actuation modes. These mechanisms can change the way they are actuated without adding additional actuators, but this change can only be carried out when the mechanism is stopped, thus increasing the time necessary to perform the task.
• Planning working mode changing trajectories. The main way to proceed is to cross a Type 1 singularity by reaching the workspace boundary and changing the leg configuration. By changing the leg configuration, the singularity loci appearing in the workspace for the initial configuration disappear and are replaced by other singularity loci linked to the new leg configuration. Thus, the robot is able to access new workspace zones. It should be mentioned that:
  • Type 1 singularities are a special type of serial singularities due to the degeneracy of the leg twist systems including active joint twists.
    
  • For the moment, changing the leg configuration by crossing a LPJTS singularity has not been investigated, even if this process could allow accessing new workspace zones.
    
• Planning assembly mode changing trajectories. A first way to do this is to bypass a cusp point. However, this solution is hardly practical for two main reasons: i) it forces the mechanism to follow a particular trajectory, which can be very different from the desired one; ii) only a few mechanisms have cusp points. A second solution is to go directly through a Type 2 singularity.

The two last solutions (that could be combined or not) are promising, since they can considerably increase the workspace size of any parallel mechanism by using only trajectory planning approaches.

As a result, I have provided a physical criterion for changing assembly modes by passing through the Type 2 singularities, which has been obtained through the analysis of the degeneracy conditions of the parallel robot Inverse Dynamic Model (IDM). This criterion enables the computation of a trajectory which can cross a Type 2 singularity without the dynamic model degenerating, by respecting the criterion in question on the singularity locus. Experimental results on a spatial four degrees-of-freedom parallel robot named the PAMINSA (Figs. 1-2) validated the proposed theory.

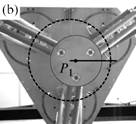
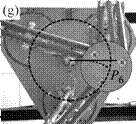
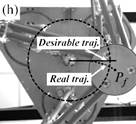
Fig. 1. Trajectory reproduction on the PAMINSA during the displacement of the platform through a singular configuration without taking into account the condition of model non-degeneracy (view from below): the robot fails on moving along the trajectory.

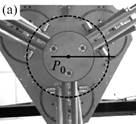
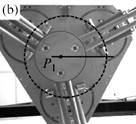
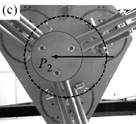
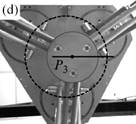
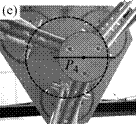
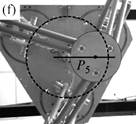
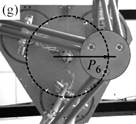
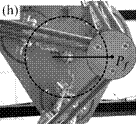
Fig. 2. Trajectory reproduction on the PAMINSA during the displacement of the platform through a singular configuration when taking into account the condition of model non-degeneracy (view from below): the robot succeeds on crossing the singularity.

More details in

S. Briot and V. Arakelian, "Optimal Force Generation of Parallel Manipulators for Passing through the Singular Positions," The International Journal of Robotics Research, 2008, Vol. 27, No. 8, pp. 967-983.

S. Briot, G. Pagis, N. Bouton and P. Martinet, "Degeneracy Conditions of the Dynamic Model of Parallel Robots,"Multibody System Dynamics, 2015, accepted.

2. Definition of advanced controllers for robust singularity crossing

In order to correctly track a trajectory, only a dynamic control law can be used since only can control the accelerations. Moreover, it is the only kind of control law that takes into account the dynamic properties of the system. Among the different dynamic control loop algorithms, the most efficient one is probably the Computed Torque Control (CTC). It computes the actuator torque of the robot based on its dynamic model and the desired trajectory. However, this control law is sensitive to modeling errors, so the dynamic model must be well identified (see Sections on Model Identification).

Furthermore, to be used when crossing a Type 2 singularity, the dynamic model must not degenerate near singularities, even if the trajectory does not perfectly respect the physical criterion mentioned above, which is unavoidable with usual CTC. As a result, we have proposed a new multi-model CTC (Fig. 3) which guarantees that the robot dynamic model of the mechanism does not degenerate near a singularity. In Fig. 3:

• M is the mass matrix and H the vector of Coriolis and centrifugal efforts of the full robot dynamic model
• M' is the mass matrix and H' the vector of Coriolis and centrifugal efforts of a non-degenerated modified dynamic model
• sigma is a function depending of the proximity to Type 2 singularities: sigma = 0 far from singularity, sigma = 1 inside the singularity

This multi-model control law was developed thanks to the definition of a new dynamic criterion based on the one presented in the Section on the Degeneracy Conditions for the Parallel Robot Dynamic Model.

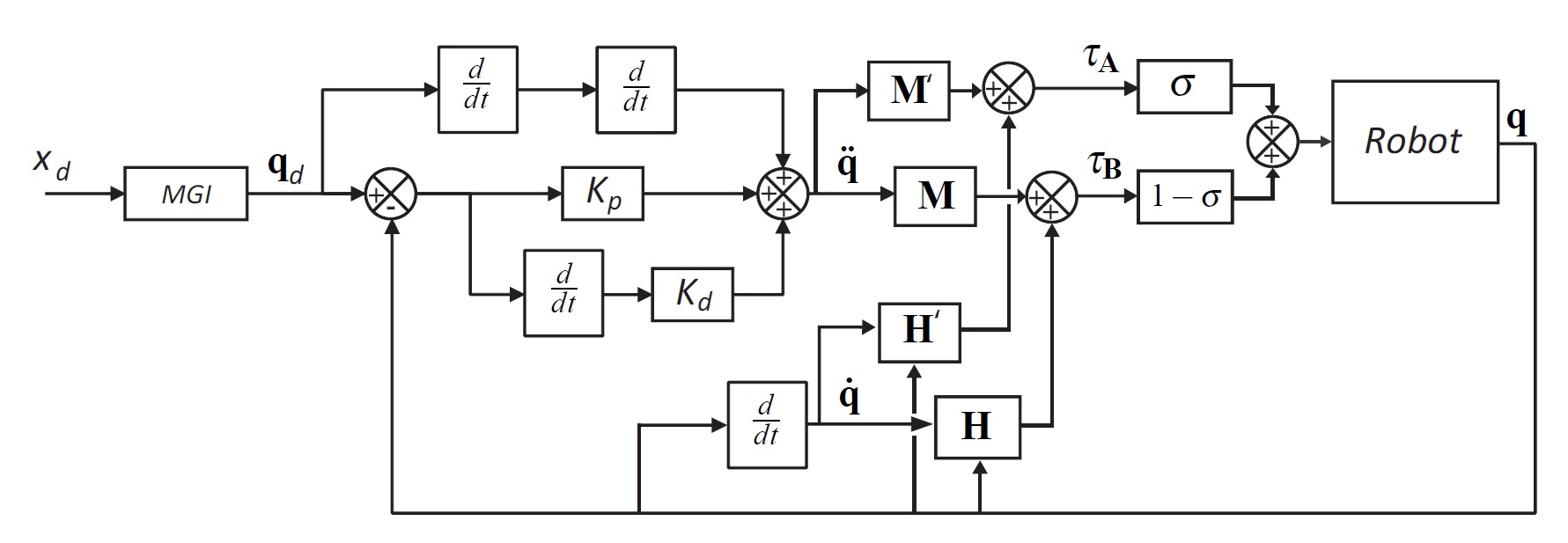
Fig. 3. New multi-model control approach for passing through the singular configurations.

Experimental results, made on a prototype of Five-bar mechanism (Fig. 4) designed and manufactured at IFMA (France) have shown that the new multi-model control approach was robust (tests were performed on three different trajectories run 5 times each) and allows without any failure the crossing of the Type 2 singular configurations (Fig. 5), while the usual CTC approach does not succeed to do it (Fig. 6).

Fig. 4. Prototype of Five-bar mechanism designed and manufacture at IFMA.

Fig. 5. Prototype of Five-bar mechanism using the new multi-model control approach (succeed in passing through the singularity).

Fig. 6. Prototype of Five-bar mechanism using the usual CTC approach (fails in passing through the singularity).

This approach has been successfully applied to several robots, such as the DexTAR of the ETS and the DexTAR of Mecademic.

More details can be found in

G. Pagis, N. Bouton, S. Briot and P. Martinet, "Design of a Controller for Enlarging Parallel Robots Workspace through Type 2 Singularity Crossing," Proceedings of 2014 IEEE International Conference on Robotics and Automation (ICRA 2014), May 31 - June 5, 2014, Hong Kong, China.

G. Pagis, N. Bouton S. Briot and P. Martinet, "Enlarging Parallel Robot Workspace through Type-2 Singularity Crossing," Control Engineering Practice, 2015, Vol. 39, pp. 1-11