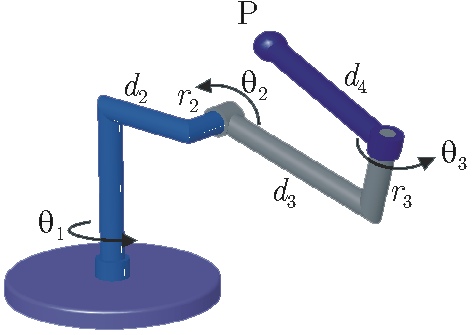
Robot 3R à axes orthogonaux
La plupart des robots industriels ont une architecture de type anthropomorphe (un axe vertical suivi de deux axes parallèles, et un poignet à axes concourants) dont les propriétés cinématiques sont bien maîtrisées offrent peu de place à l’optimisation des performances. Le but de nos travaux est l’étude de cinématiques alternatives pouvant offrir de nouvelles propriétés ou permettant de réduire les coûts de fabrication des robots. Nous étudions en particulier une famille de robots d’axes orthogonaux.
Nous collaborons avec l’IRMAR et l’INRIA dans le cadre
d’un projet « MathStic » pour la classification des
robots orthogonaux. Cette classification repose sur la topologie des
singularités dans une section génératrice de l’espace
de travail.
Cette topologie peut être caractérisée par le nombre
de points cusps (correspondant à trois solutions inverse identiques)
et de points doubles (une paire de deux solutions identiques). Ces points
singuliers servent à définir des propriétés
importantes comme la répartition des solutions inverses dans
l’espace de travail (régions à nombre de solution
donné, présence de trous), la cuspidalité (le fait
que les solutions inverses ne sont pas séparées par une
singularité dans l’espace articulaire).
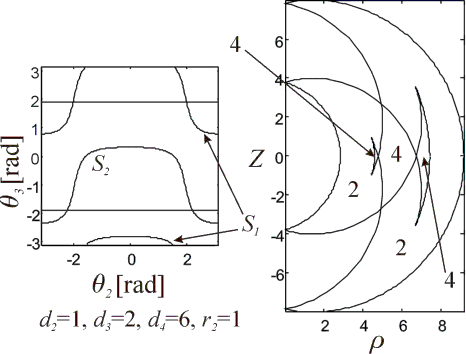
Exemple: Singularités dans l’espace articulaire (à gauche) et dans une section génératrice de l'esapce de travail (à droite, on remarque la présence de 4 points cusps et 4 points doubles. Les chiffres correspondent au nombre de solutions inverse dans chaque région)
On montre que l’espace des robots orthogonaux se décompose en neuf domaines où le nombre de point cusp est constant. Nous connaissons l'expression analytique des frontières entre chaque domaine de l'espace des paramètres de DH.
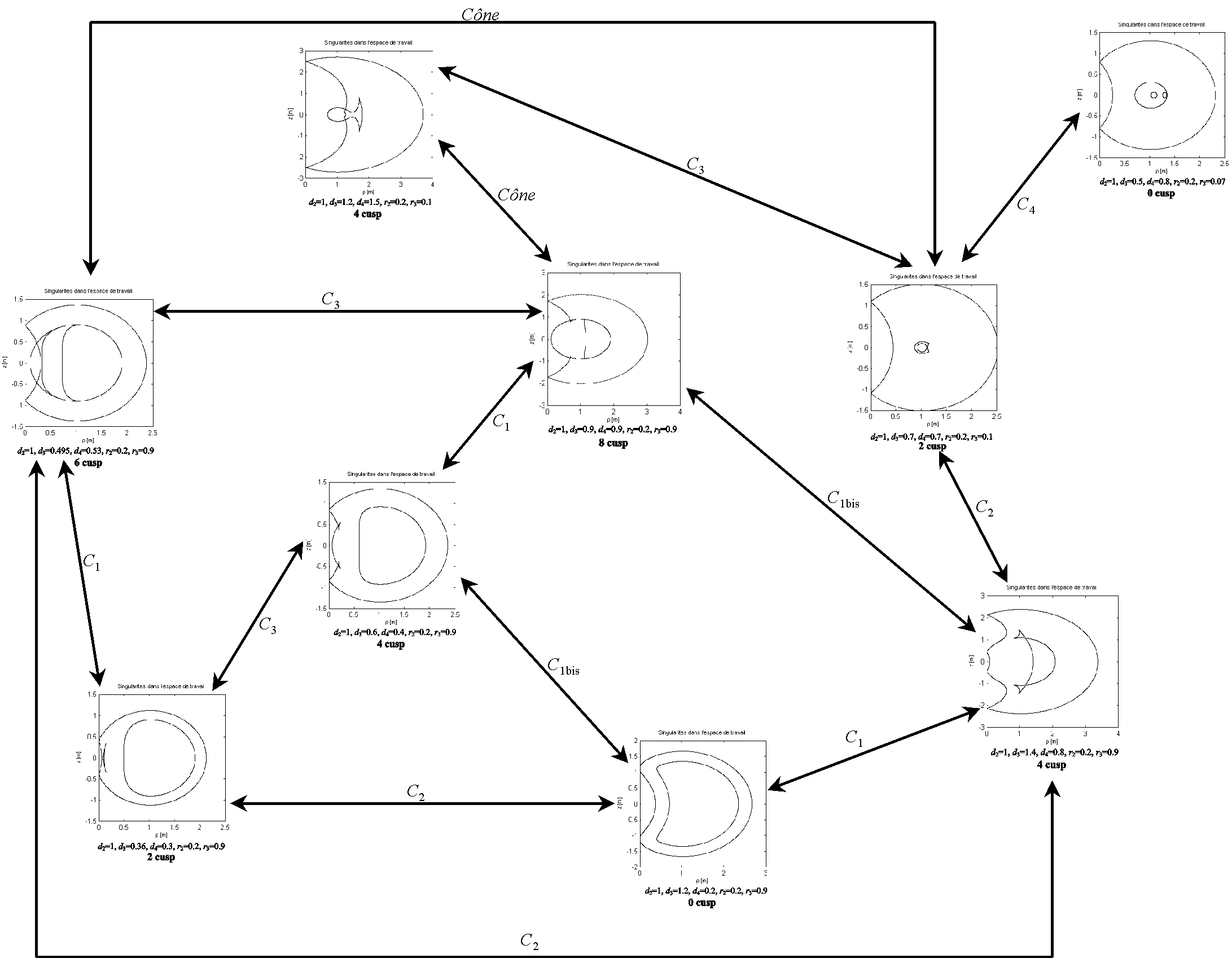
Une étude similaire est en cours pour caractériser les topologies d'espace de travail ayant un nombre de points cusp et de node constant.
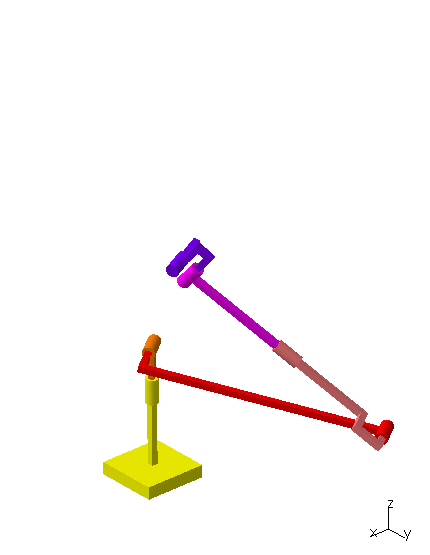 (avi)
(avi)
Animation pour montrer une position de l'effecteur possédant 12 solutions au modèle géométrique inverse.