Damien Chablat

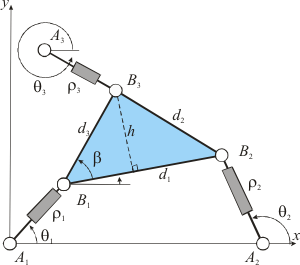
Kinematic analysis of a a planar 3-RPR parallel manipulators

Article written by Guillaume Moroz, Fabrice Rouiller, Philippe Wenger and Damien Chablat during the SiRoPa project.

> with(LinearAlgebra): with(VectorCalculus):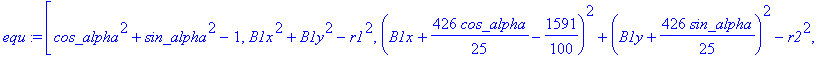
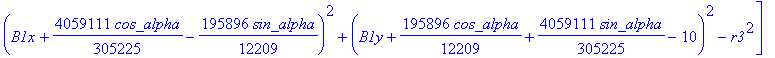
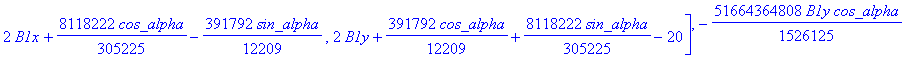
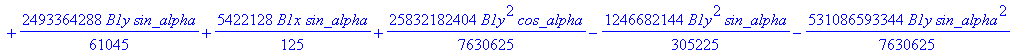
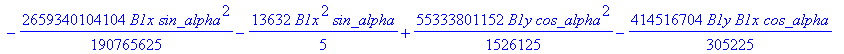
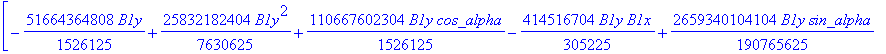
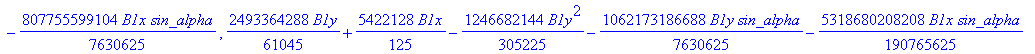
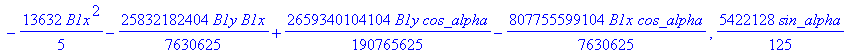
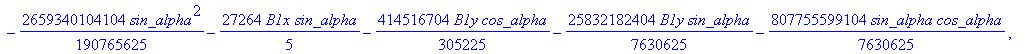
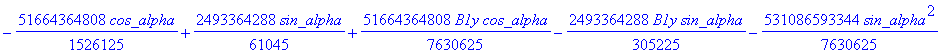
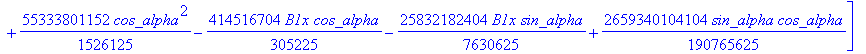
> equ :=
 [ cos_alpha^2+sin_alpha^2-1,
    B1x^2+B1y^2-r1^2,
    (B1x+426/25*cos_alpha-1591/100)^2+(B1y+426/25*sin_alpha)^2-r2^2,
    (B1x+4059111/305225*cos_alpha-195896/12209*sin_alpha)^2+
    (B1y+195896/12209*cos_alpha+4059111/305225*sin_alpha-10)^2-r3^2 ];

s > m, j := Jacobian (equ, vCusp, determinant);

> mCusp := Jacobian ([op(equ),j], vCusp);

 

cusp := [ op(equ), j, Determinant (SubMatrix (mCusp,[1,2,3,5],[1..4])),
                      Determinant (SubMatrix (mCusp,[1,2,4,5],[1..4])),
                      Determinant (SubMatrix (mCusp,[1,3,4,5],[1..4])),
                      Determinant (SubMatrix (mCusp,[2,3,4,5],[1..4]))  ];

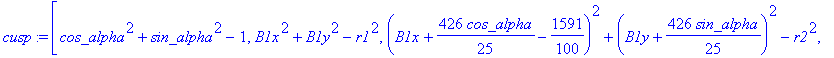
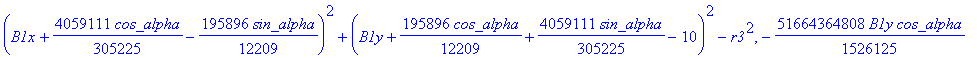
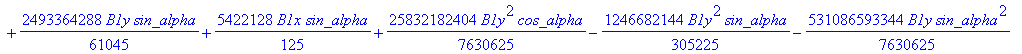
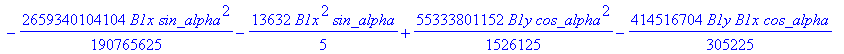
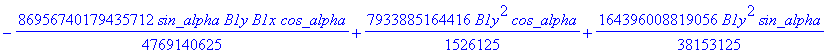
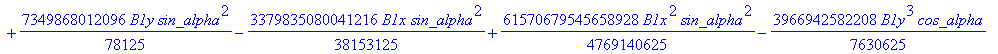
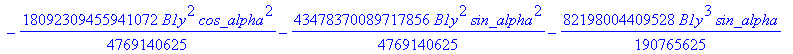
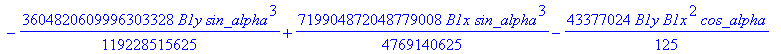
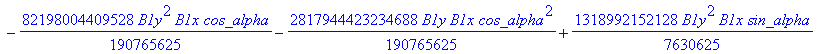
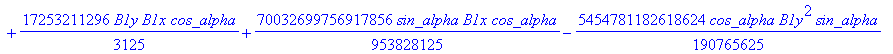
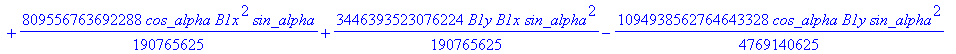
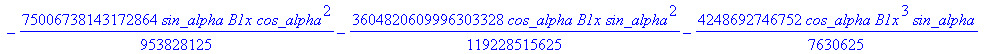
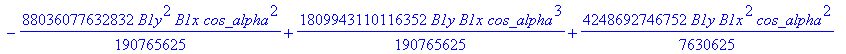
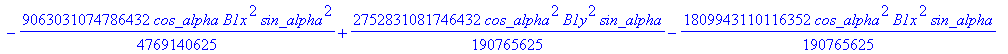
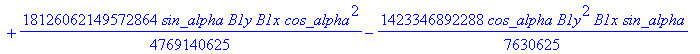
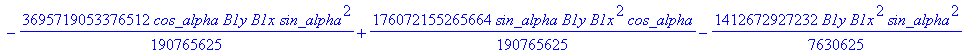
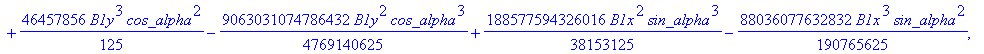
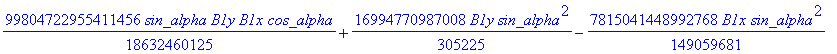
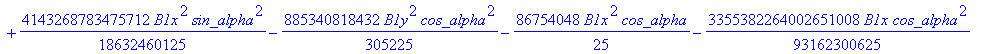
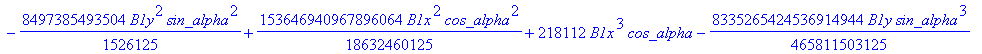
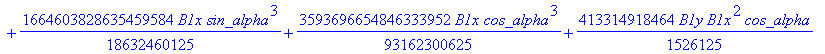
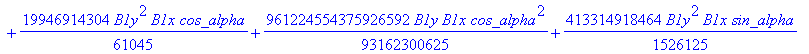
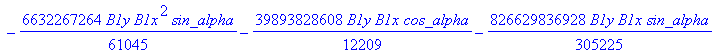
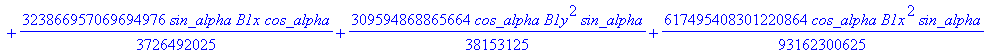
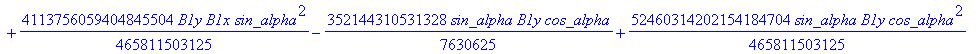
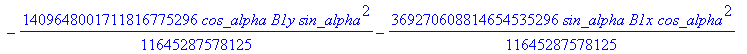
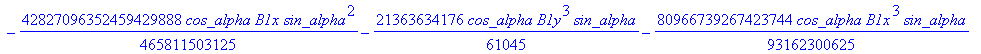
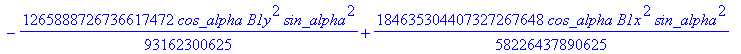
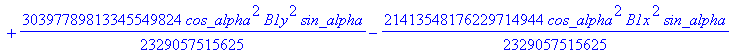
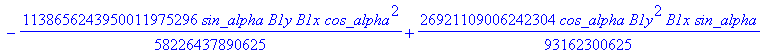
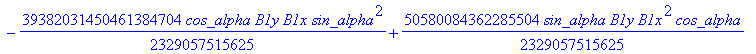
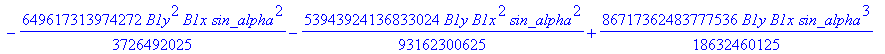
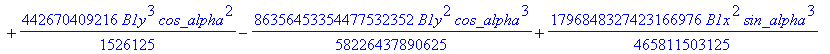
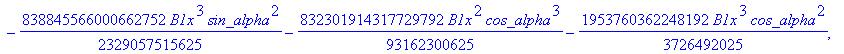
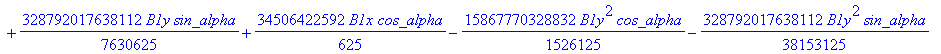
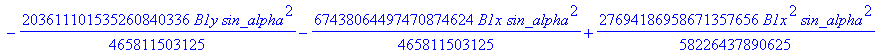
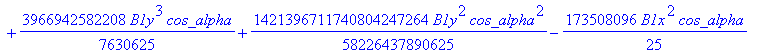
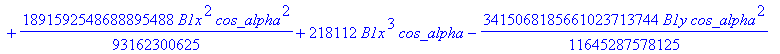
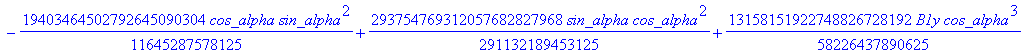
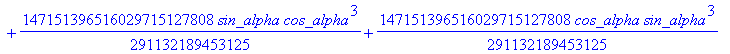
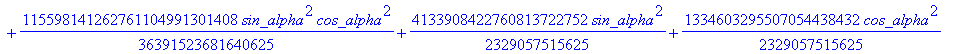
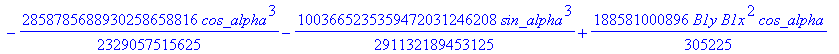
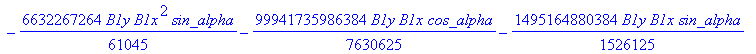
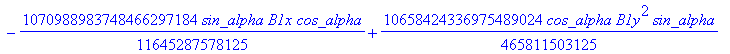
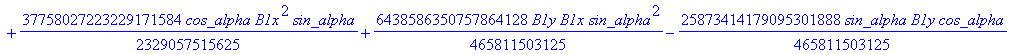
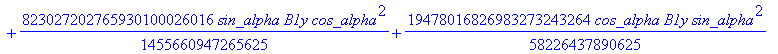
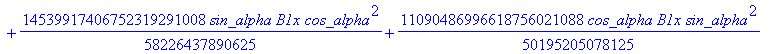
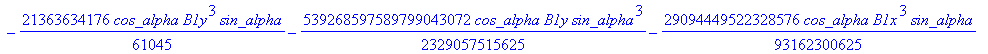
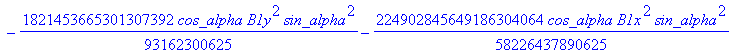
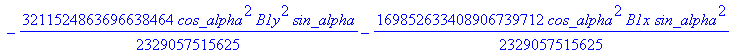
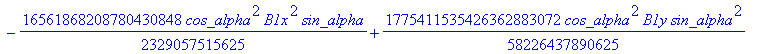
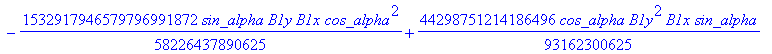
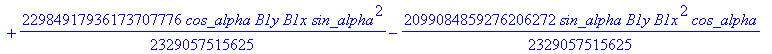
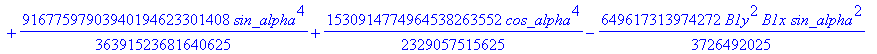
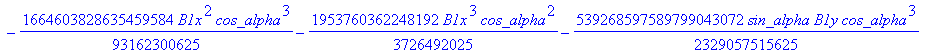
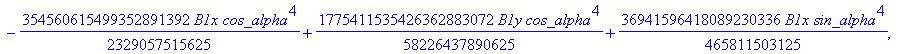
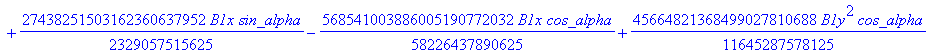
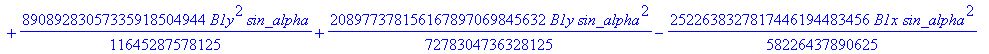
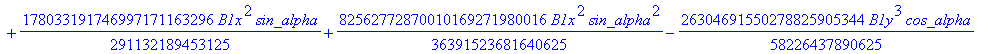
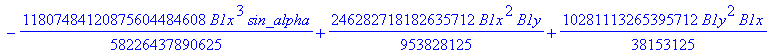
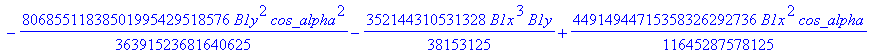
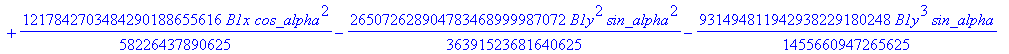
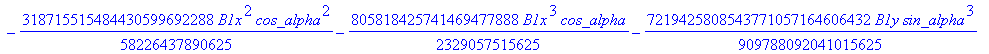
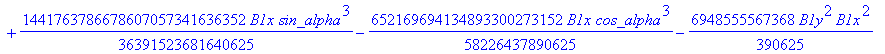
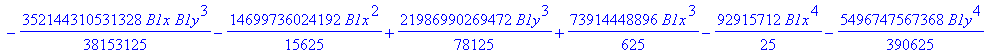
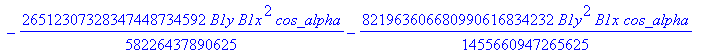
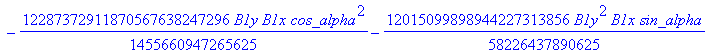
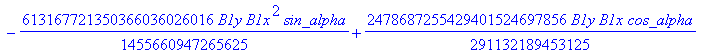
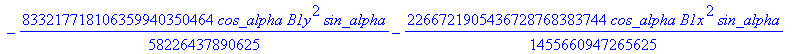
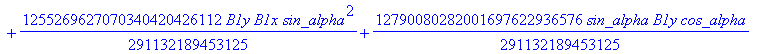
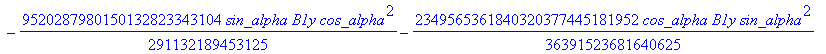
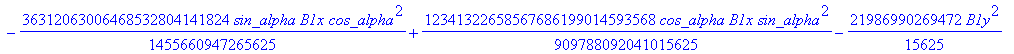
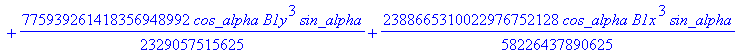
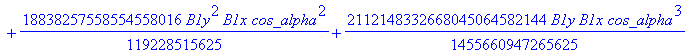
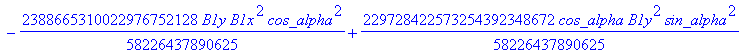
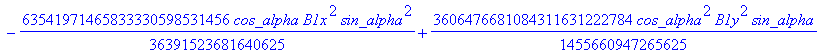
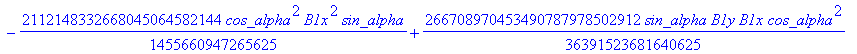
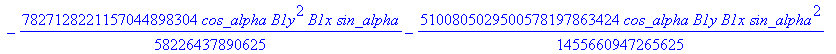
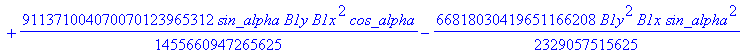
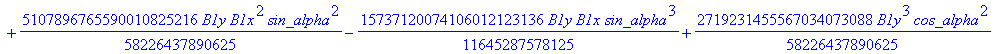
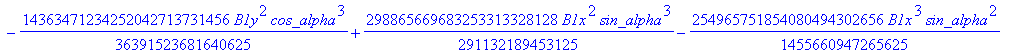
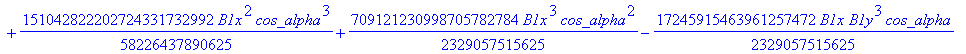
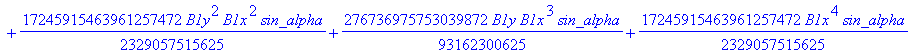
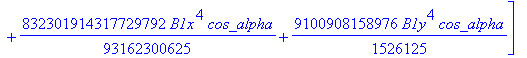
Computation of the discriminant variety of the cusp curves

> pDv  := [r1];
> vDv := [cos_alpha, sin_alpha, B1x, B1y, r2, r3];

 

> mDv := Jacobian (cusp, vDv);

> equDv := [ op(cusp),
           op( map (l->Determinant (SubMatrix (mDv,l,[1..6])),
                    combinat:-choose ([1,2,3,4,5,6,7,8,9], 6)) ) ]:

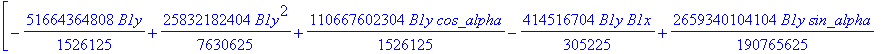
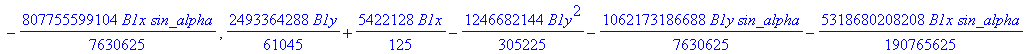
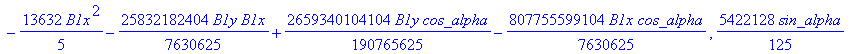
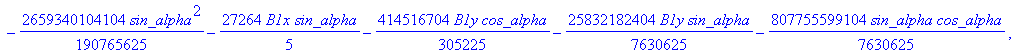
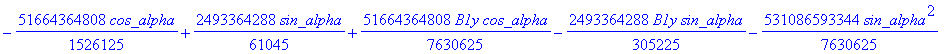
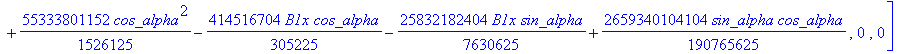
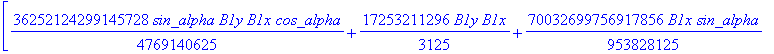
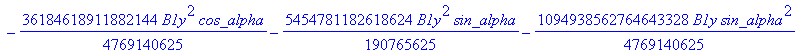
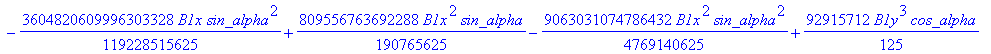
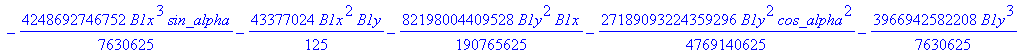
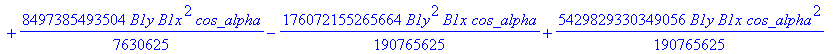
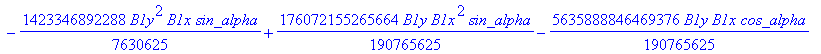
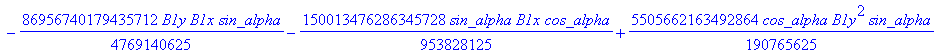
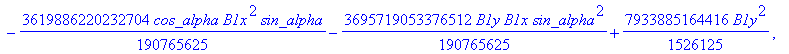
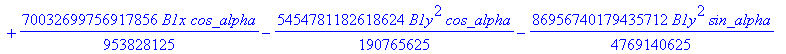
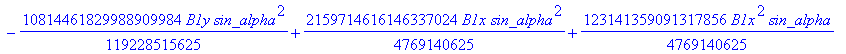
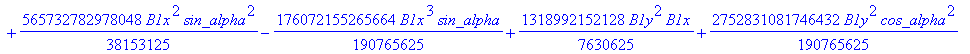
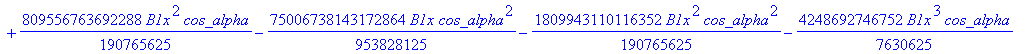
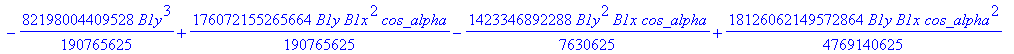
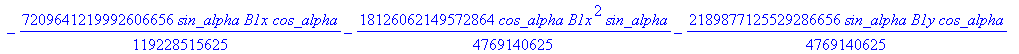
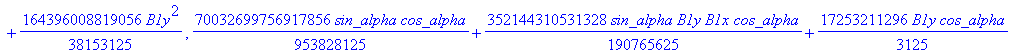
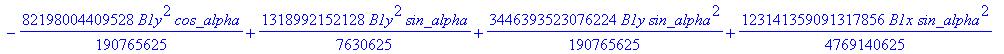
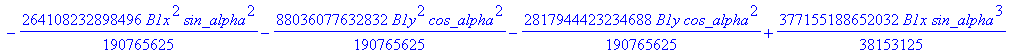
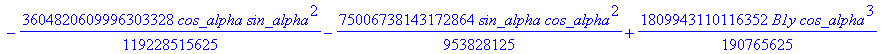
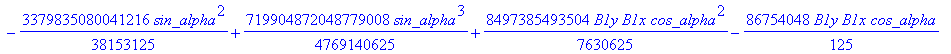
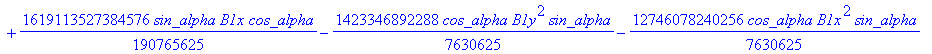
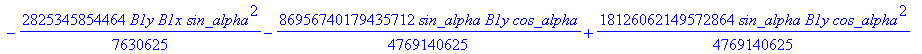
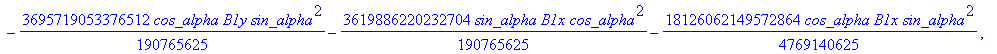
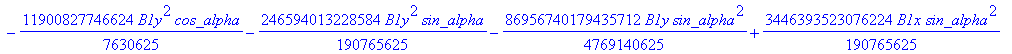
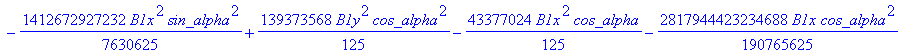
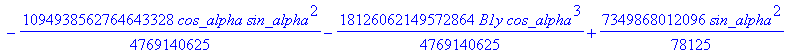
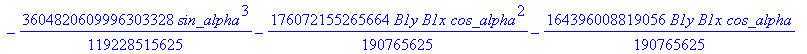
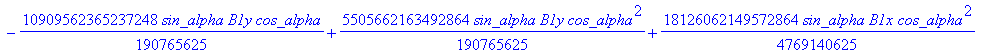
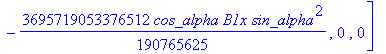
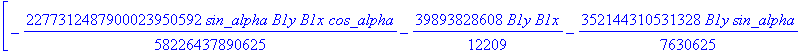
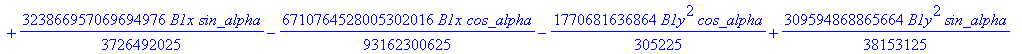
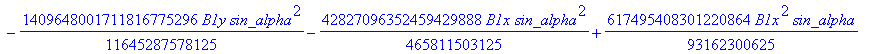
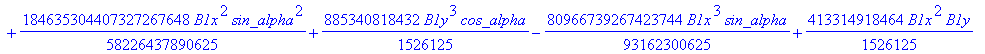
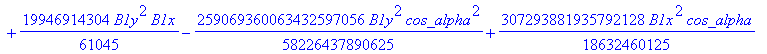
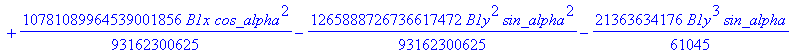
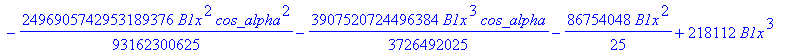
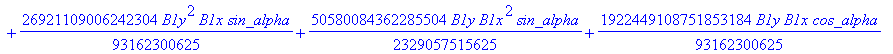
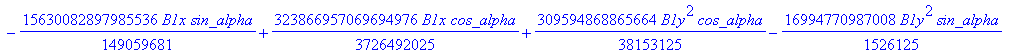
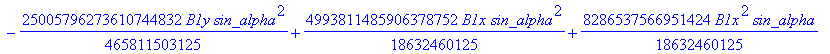
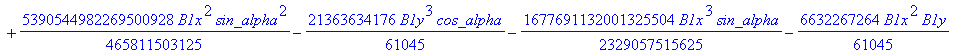
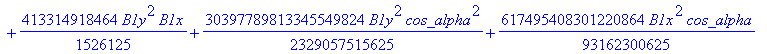
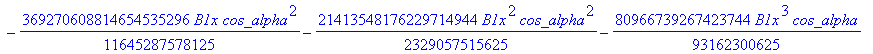
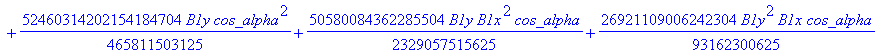
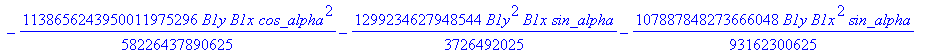
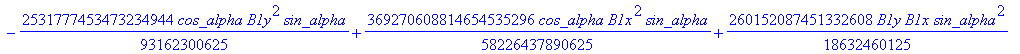
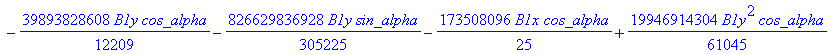
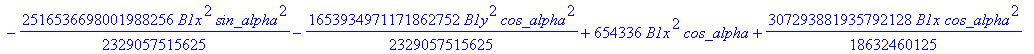
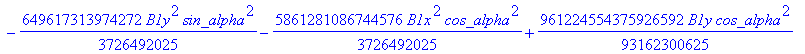
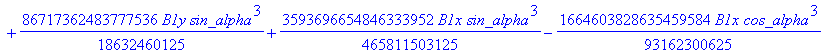
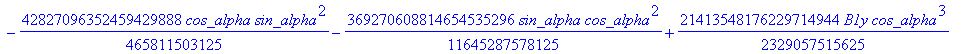
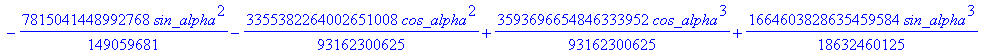
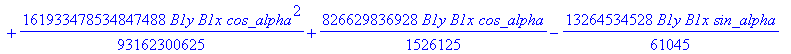
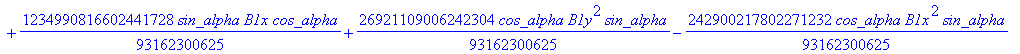
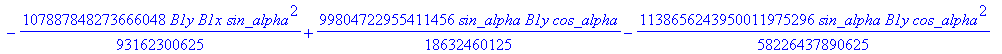
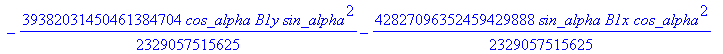
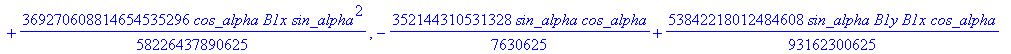
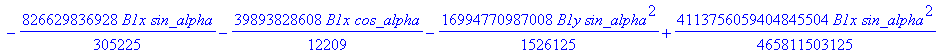
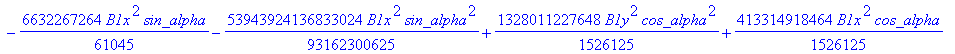
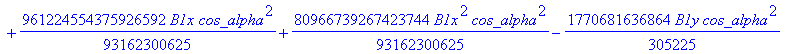
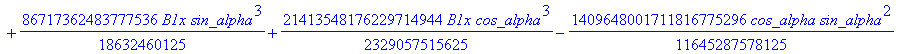
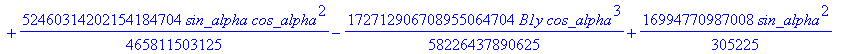
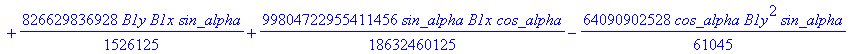
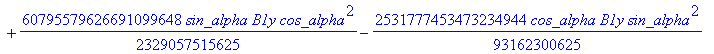
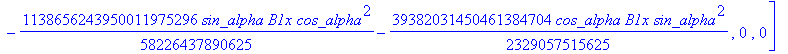
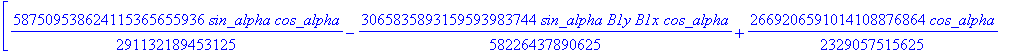
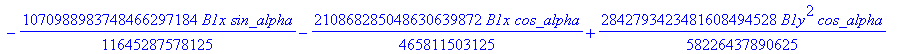
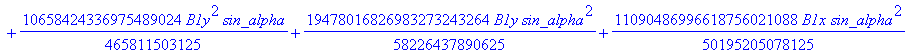
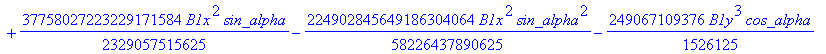
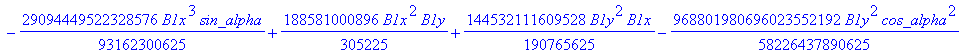
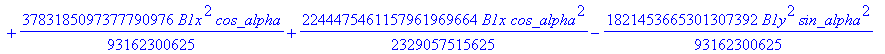
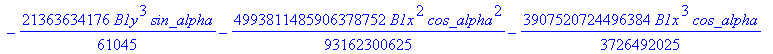
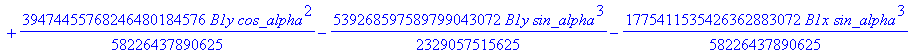
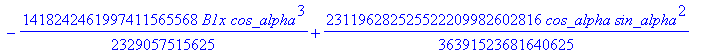
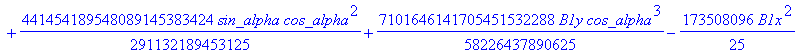
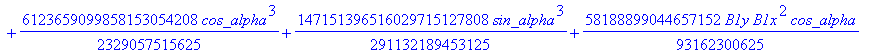
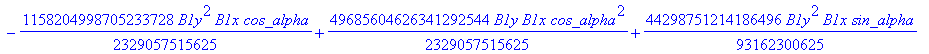
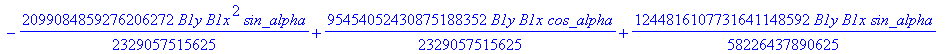
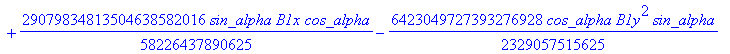
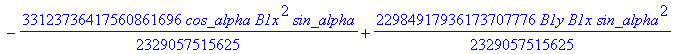
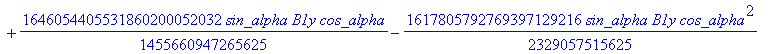
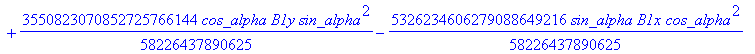
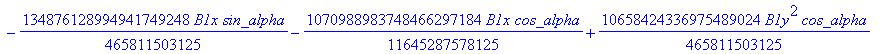
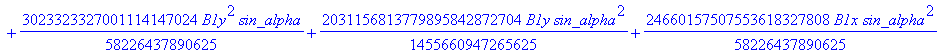
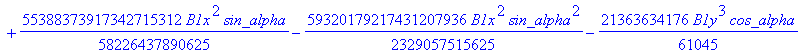
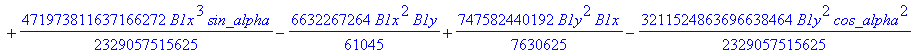
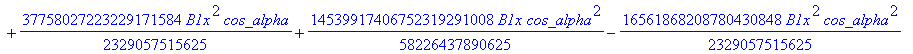
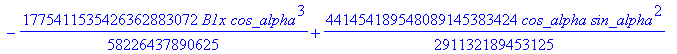
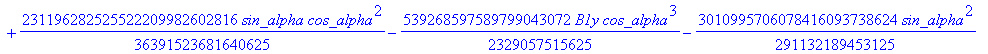
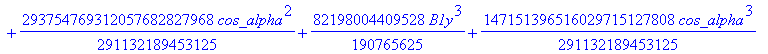
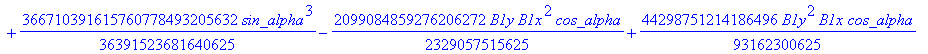
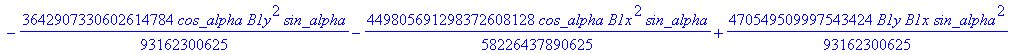
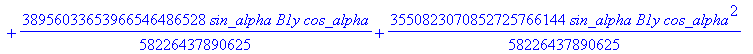
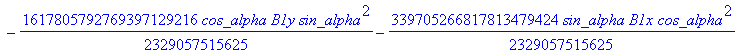
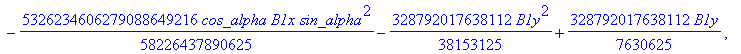
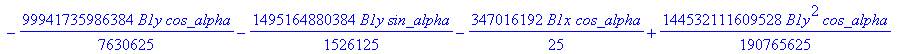
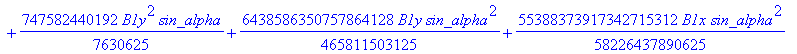
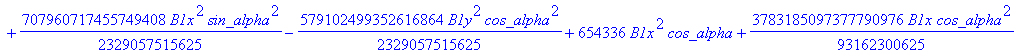
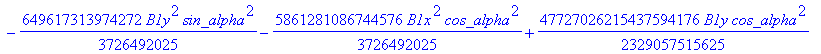
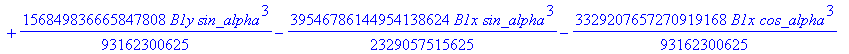
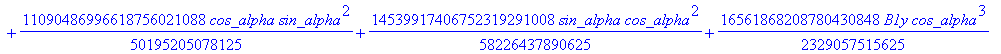
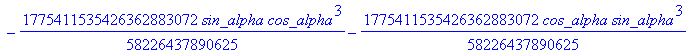
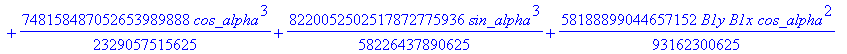
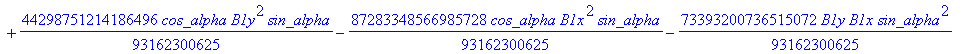
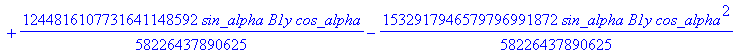
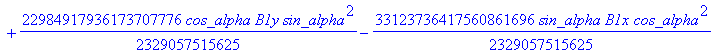
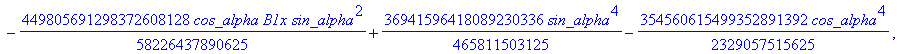
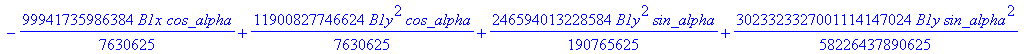
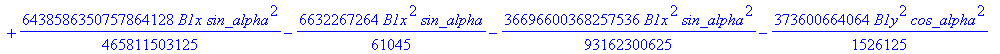
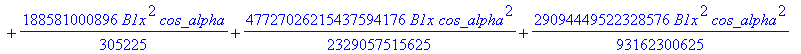
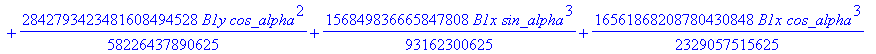
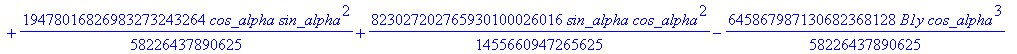
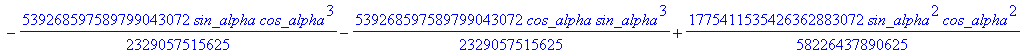
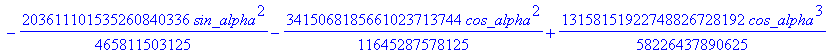
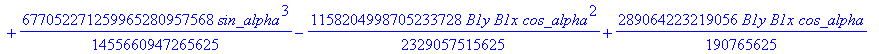
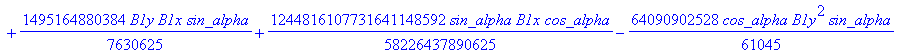
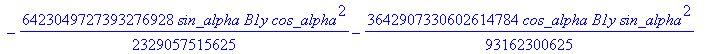
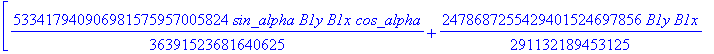
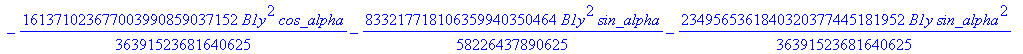
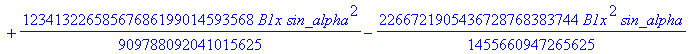
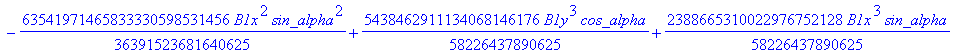
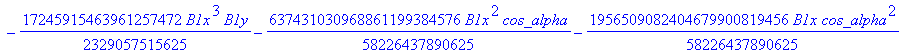
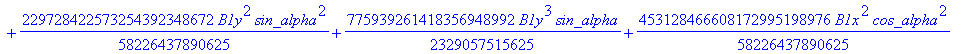
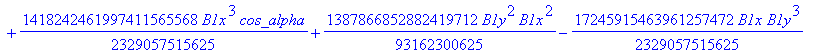
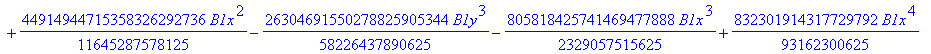
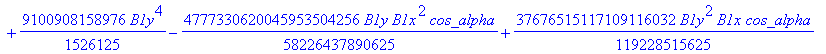
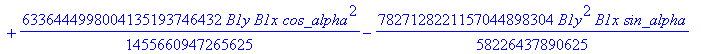
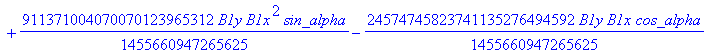
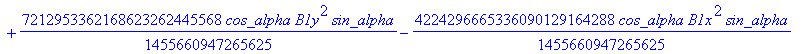
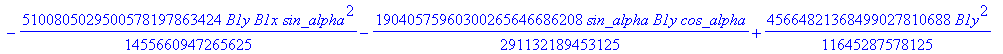
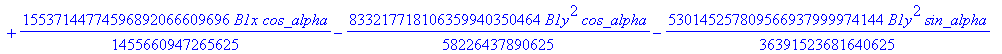
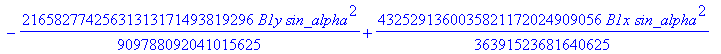
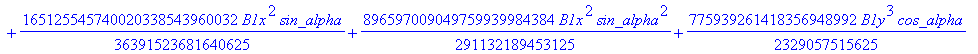
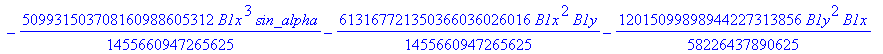
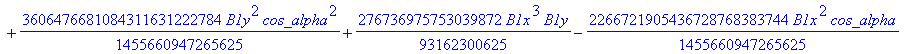
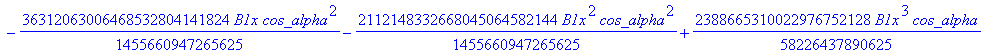
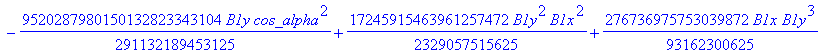
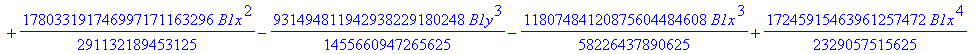
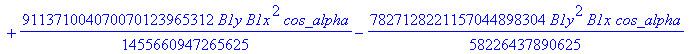
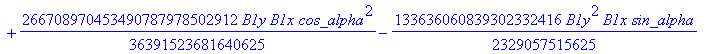
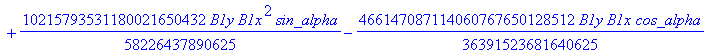
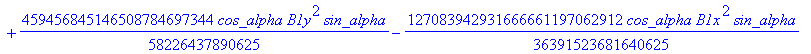
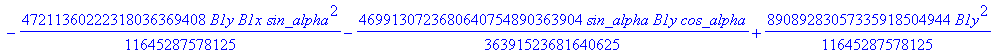
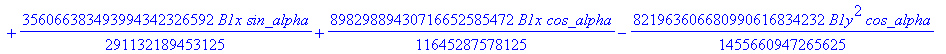
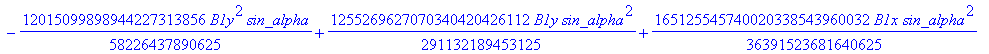
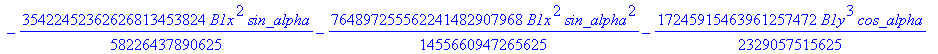
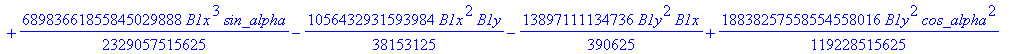
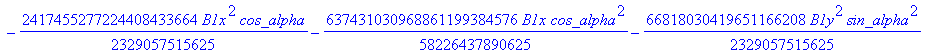
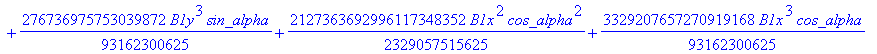
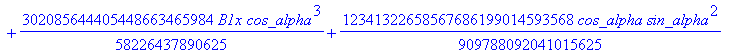
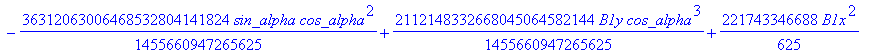
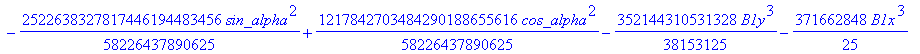
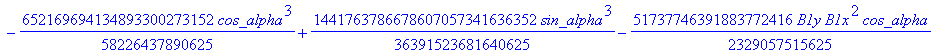
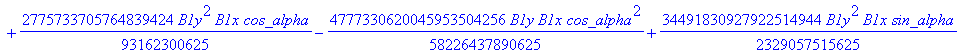
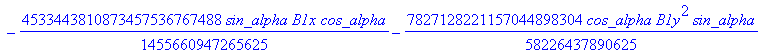
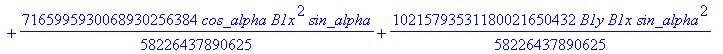
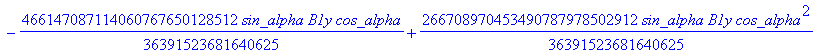
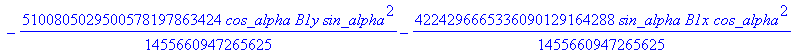
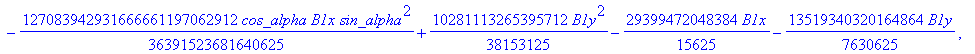
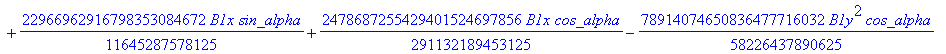
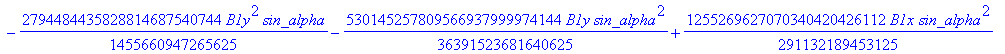
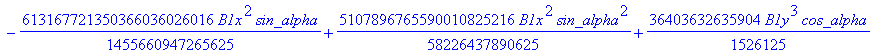
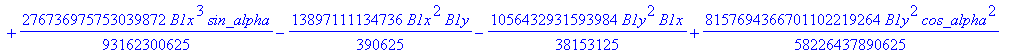
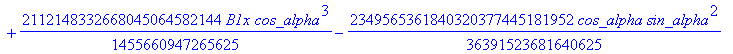
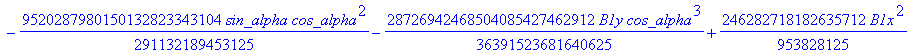
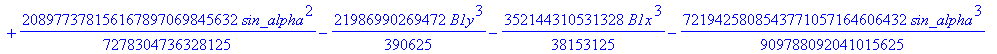
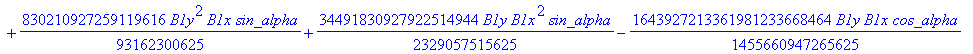
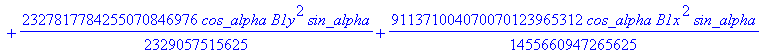
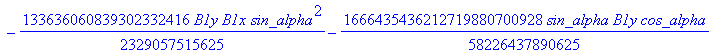
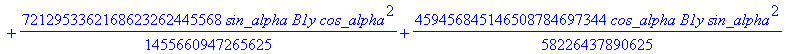
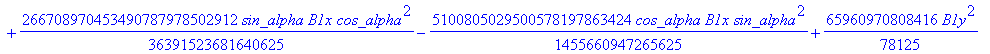
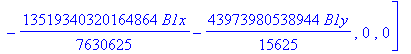
> dv := fgbrs:-fgb_gbasis (expand(numer(equDv)), vDv, pDv, 0, "elim force"=true, "verb"=false)[1][3]:

Discriminant variety of the cuspidal configurations

> RootFinding:-Isolate ( dv, [r1] );